WIKI Experimental design optimization
This section describes how to optimize the experimental design with the aim of either estimating model parameters or comparing models. First, we recall the definition of design optimality scores. Then, we suggest on-line extensions to the approach for adapative design strategies.
Design optimality scores
Optimizing the design in the context of, e.g., experimental psychology studies, amounts to identifying the subset of conditions and stimuli (\(u\)) that yields the highest statistical power, under a variety of practical constraints. This requires being able to predict experimental data under models’ assumptions, including potential confounds that may mask the effects of interest. Design optimization can become a difficult issue whenever the impact of experimental factors onto measurements (through the model) is non-trivial and/or uncertain (cf. unknown model parameters). This motivates the use of automatic design optimization.
The VBA toolbox can handle two classes of problems, namely optimizing the system’s input \(u\) with respect to either parameter estimation or model selection. These two problems correspond to two different objectives, which can be formalized in terms of statistical loss functions:
Parameter estimation
How should one set the inputs \(u\), such that measured experimental data eventually yield accurate parameter estimates? One first has to define “estimation accuracy”. Let \(\hat{\theta} = E \big[ \theta\mid y \big]\) be the posterior estimate of unknown model parameters \(\theta\), given experimental data \(y\). Estimation error induces a statistical loss, which increases with the distance between \(\hat{\theta}\) and \(\theta\). The expected squared estimation error is given by:
\[E \big[( \hat{\theta} -\theta)^2 \mid y \big] = V \big[ \theta\mid y \big]\]where \(V \big[ \theta\mid y \big]\) is the posterior variance over the unknown model parameter \(\theta\). Thus, maximzing estimation accuracy reduces to minimizing a posteriori variance. This intuition generalizes to models with more than one parameter. In this case, one usually minimizes the trace of the expected posterior matrix (cf. so-called “A-optimality”). Note that, for non-linear generative models, the posterior variance will depend upon the (not yet observed) data \(y\). One then needs to derive the expected posterior variance, where the expectation is taken under the marginal distribution of the data. This can be done by evaluating the design efficiency for each design, as follows:
e = VBA_designEfficiency(f_fname,g_fname,dim,options,u,'parameters')
where u is the time series of experimental control variables (inputs) that defines the design and e is the design efficiency (minus the trace of the expected posterior covariance matrix).
Have a look at demo_designOptimization.m for an example of implementation.
Model selection
Now how should one set the inputs \(u\), such that measured experimental data eventually best discriminates between candidate models? In this context, one should choose among experimental designs according to their induced model selection error rate. Let \(\hat{m}\) be the selected model (according to the criterion of Bayesian model comparison). The statistical loss of a model selection can be defined as the binary error \(e\):
\[e = \left\{ \begin{array}{ll} 1 \textrm{ if } \hat{m}=m \\ 0 \textrm{ otherwise} \end{array} \right.\]As for parameter estimation, one can derive a posterior estimate of this error, i.e.: \(P\big(e=1 \mid y,u \big)\). In turn, prior to the experiment, on can derive the expected model selection error rate:
\[P\big(e=1 \mid u \big) = \int_Y{ P\big(e=1 \mid y,u \big) p\big(y \mid u \big) dy }\]where the expectation is taken under the marginal likelihood \(p\big(y \mid u \big)\). Of course, the expected model selection error rate increases with the similarity of model predictions:
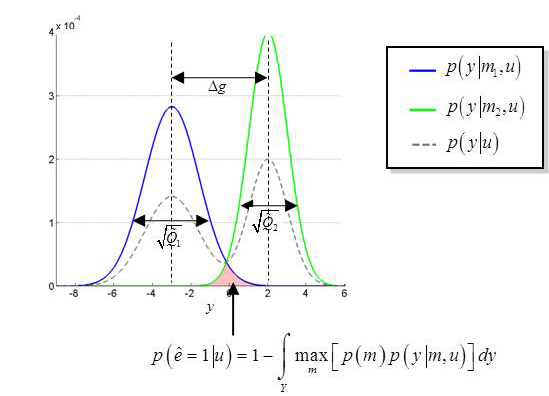
Here, prior predictive densities (y-axis) of two different models are plotted over possible data values (x-axis; unidimensional data). Although no analytical expression for the selection error rate exists, one can derive the the so-called “Laplace-Chernoff risk” \(b_{LC}\), which measures the statistical similarity of the prior predictive densities, as a function of their 1st- and 2nd-order moments:
\[b_{LC}(u) = 1-\frac{1}{2}\log\:\left(\frac{\Delta g(u)^2}{4\tilde Q(u)}+1\right) \quad \text{if}\; \tilde Q_1(u) \approx \tilde Q_2(u) \equiv \tilde Q_(u)\]It turns out that the Laplace-Chernoff risk provides an upper bound on the selection error rate (Daunizeau et al. 2011). Thus, optimizing the experimental design w.r.t. model selection reduces to choosing the input \(u\) that minimizes the Laplace-Chernoff risk \(b_{LC}\). In VBA, the numerical derivation of design efficiency for model comparison can be done as follows:
[e,out] = VBA_designEfficiency(f_fname,g_fname,dim,options,u,'models')
where f_fname, g_fname, dim, options are nx1 cell arrays (n models), e is design efficiency (i.e. minus the Chernoff risk) and out is a structure containing diagnostic variables (e.g., 1st- and 2nd-order moments of the Laplace approximation to the prior predictive density..).
One can then either compare different designs on the basis of their efficiency (e.g. on a predefined set of inputs \(u\)), or perform numerical optimization of the design efficiency w.r.t. \(u\) (or some parametric form of it).
Online adaptive designs
In the context of, e.g., experimental psychophysics, adaptive designs such as “staircase” methods are typically used to estimate some individual sensory detection or discrimination threshold. Such procedures operate in real-time in the sense that the next stimulation depends on the previous behavioral response and is computed in order to optimize model fitting. More generally, adaptive (online) designs can be used to improve on three problems: (i) model parameter estimation; (ii) hypothesis testing (or BMS); (iii) choosing the duration of the experiment (e.g., the number of trials).
Practical application
We have implemented an example of offline and online adaptive design in the demonstration script demo_designOptimization.m. This demo simulates a psychophysics paradigm similar to a signal detection task, whereby the detection probability is a sigmoidal function of the stimulus contrast (which is the design control variable). The goal of the dummy experiment is to estimate the sigmoid’s inflexion point (detection threshold) and the sigmoid’s slope (aka d-prime). Here, the design is adapted either offline or online in the aim of providing the most efficient estimate of these model parameters, either before the experiment (offline) or given trial-by-trial (online) subjects’ binary choice data (y=1: “seen”, y=0: “unseen”).
No optimization
On the upper graph, one can see the histogram of stimulus intensity presentation. Without optimization, one strategy is simply to present all possible intensities an equal number of times (left).
The middle left graph shows the subject’s responses (black dots) simulated using a known psychometric model (green), and the estimated response curve, in terms of the detection probability (y-axis) as a function of stimulus contrast (x-axis).
On the bottom-left graph, one can see the true value (green dots) and the posterior estimates of the model parameters. These converge around the simulated values.
Offline optimization
In the center plots, we first generate a large number of random designs (ie. random sequences of stimulus intensities). Keeping only designs of increasing efficiency (blue curve, 2nd line of plots), one can see that the design is most efficient when the sigmoid function is sampled around the expected maximal curvature regions, ie. on both sides of the expected inflection point (here: 0). As the exact position of this inflection point is not know in advance, a rather large range of stimulus intensities needs to be presented.
Online optimization
For online optimization, the stimulus intensity is selected trial-by-trial. The upper right plot shows the design efficiency (blue line, right y-axis) as a function of stimulus contrast (x-axis) for the upcoming trial. The histogram of the previously presented intensities essentially focuses the sigmoid sampling at the maximal curvature regions, ie. around the estimated (so far) inflection point.
Note that the experiment could have been stopped before (after about 40 trials), on the basis of the convergence of the design efficiency score. Early-stopping rules can be enforced by setting a threshold on design efficiency, in the aim of performing short and efficient experiments…
