WIKI Setting the priors through Empirical Bayes
Setting the priors is arguably one of the most delicate issues of Bayesian inference. Although only flat priors are valid from a frequentist perspective, they are in fact largely suboptimal, when compared to almost any form of informative prior. The reason lies in the so-called “bias-variance trade-off” of statistical estimation: the systematic bias that may be induced by informative priors is overcompensated by the reliability of regularized parameter estimates. In brief, if one really cares about expected estimation error, then one should not aim for unbiasedness…
But acknowledging the benefit of priors does not solve the issue of setting them, in the commonplace situation where one does not have much solid ground to lay on. This is where so-called empirical Bayes methods may be useful. In brief, these are procedures for statistical inference in which the prior distribution is estimated from the data. This approach stands in contrast to standard Bayesian methods, where the prior distribution is fixed before any data are observed. In VBA, the empirical Bayes approach always relies upon a fully Bayesian treatment of a hierarchical model, of which there are two sorts. These are covered in the following sections.
Empirical Bayes for group studies: mixed-effect modelling
Let us assume that you (i) are conducting a group study, and (ii) have developped some generative model of within-subject data. VBA enables you to perform mixed-effect modelling (MFX), whereby the priors on parameters are hierarchically defined, such that subject-level parameters are assumed to be sampled from a Gaussian density whose mean and variance are unknown but match the moments of the group distribution. Here, parameters at the highest level of the hierarchical model are summary statistics of the group. The structure of the ensuing hierarchical model is depicted in the graph below:
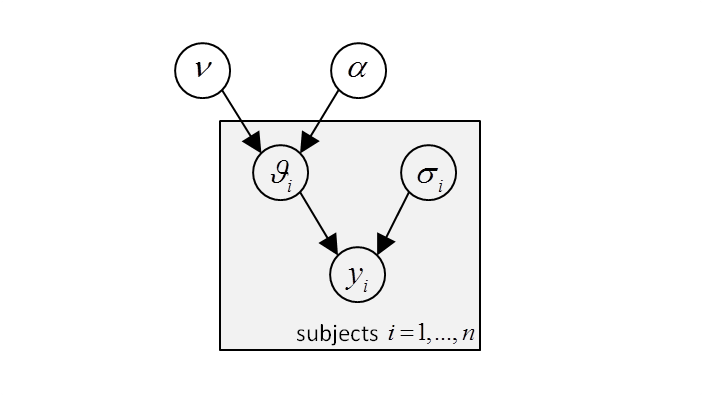
where \(\nu\) and \(\alpha\) are the unknown group summary statistics (its mean and precision, respectively), \(\vartheta_i\) is the set of unknown (evolution and observation) parameters of subject \(i\), \(y_i\) is the observed (known) data of subject \(i\) and \(\sigma_i\) is the corresponding unknown data precision. Note: the plate denotes a replication of the statistical dependencies over the group of \(n\) subjects.
Would one know the group’s summary statistics, they could be used to constrain the likely range of subject-level parameters. Reciprocally, the group’s summary statistics can be inferred from within-subject parameter estimates. This reciprocal dependency is resolved using a variational Bayesian scheme, whose pseudo-code is given below:
[LOOP UNTIL CONVERGENCE]
1) for i=1:n (loop over subjects)
define within-subject priors from group-level summary statistics
perform within-subject model inversion
end
2) update group-level summary statistics from posterior within-subject summary statistics
Over the algorithm iterations, within-subject priors are refined and matched to the inferred parent population distribution. Empirical Bayes procedures of this sort learn from group statistics, and thus inform within-subject inversions with each other results. This eventually shrinks the within-subject posterior estimate around the estimated group mean…
VBA’s main function for mixed-effect modelling is VBA_MFX.m. It is demonstrated in the demo demo_MFX.m, which exemplifies the added-value of MFX modelling in the aim of capturing between-subject variability. Note that its call is almost equivalent to VBA_NLStateSpacelModel.m:
[p_sub,o_sub,p_group,o_group] = VBA_MFX(y,u,f_fname,g_fname,dim,options,priors_group)
Its intputs and outputs are described below:
y: nsx1 cell array of observations, where ns is the number of subjects in the groupu: nsx1 cell array of inputsf_fname/g_fname: evolution/observation function handlesdim: structure containing the model dimensions.options: nsx1 cell array of options structure.priors_group: structure containing the prior sufficient statistics on the moments of the parent population distributions (for observation and evolution parameters, as well as for initial conditions, if applicable). Seep_groupsubfields below.p_sub/o_sub: nsx1 cell arrays containng the VBA outputs of the within-subject model inversions.p_group: structure containing the sufficient statistics of the posterior over the moments of the parent population distribution.o_group: output structure of the VBA_MFX approach. In particular, it contains the Free Energy of the MFX model (for model comparison purposes).
A complete mathematical description of the approach is available here.
“Agnostic” empirical Bayes approach
But what if you are performing an analysis that cannot be regularized using group data? Recall that vanilla VBA model inversion asks users to specify priors over observation and evolution parameters (as well as initial conditions). This is not to say, however, that the relative weight of priors is fixed. In fact, VBA also estimates (at least for Gaussian observations) the precision hyperparameter \(\sigma\), which quantifies the data reliability (and therefore, controls the relative weight of the likelihood on parameter estimates). This endows VBA with some flexibility, but does not cure posterior estimates from potential sensitivity to prior assumptions.
A typical advice here is to perform a sensitivity analysis, in the aim of evaluating whether, e.g., posterior credible intervals vary when priors are changed. Critical here is the fact that if data is provided with sufficient quantity/quality, then posterior inference is insensitive to priors. In turn, if the sensitivity analysis eventually concludes that posterior distributions are largely influenced by priors, then one would have to consider the possibility of acquiring more data.
Alternatively, one may wish to challenge prior assumptions in a restricted though systematic manner. For example, one may extend the idea of estimating hyperparameters to those hyperparameters that control the prior precision of (observation and evolution) model parameters. But what sort of information could be instrumental here? Well, if one knew the model parameters, one could rescale their prior variance-covariance matrix to match their set distribution. This eventually motivates the following alternative empirical Bayes approach:
[LOOP UNTIL CONVERGENCE]
1) define prior hyperparameters from set-level summary statistics and perform model inversion
2) update set-level summary statistics from posterior summary statistics
This is essentially what VBA_hyperparameters.m does. More precisely, it considers an augmented hierarchical model, whose highest level is composed of prior precision hyperparameters on observation and evolution parameters. The ensuing “agnostic” empirical Bayes approach is most appropriate when there are enough observation/evolution parameters, such that their set summary statistics (i.e. variance) can eventually be learned efficiently.
Note: in both empirical Bayes schemes, users are asked to specify “hyperpriors” (on group-level moments for MFX and on set-level hyperparameters for the “agnostic” approach). Although posterior inference will typically be less sensitive to those hyperpriors (to the point that they can be rendered flat), one may be willing to perform a post-hoc sensitivity analysis…