WIKI Spiking neuron models
This class of models attempt to capture how individual neurons respond to inputs, typically in terms of ion currents that flow through the cell membrane (this occurs when neurotransmitters cause an activation of ion channels in the cell).
Hodgkin-Huxley model
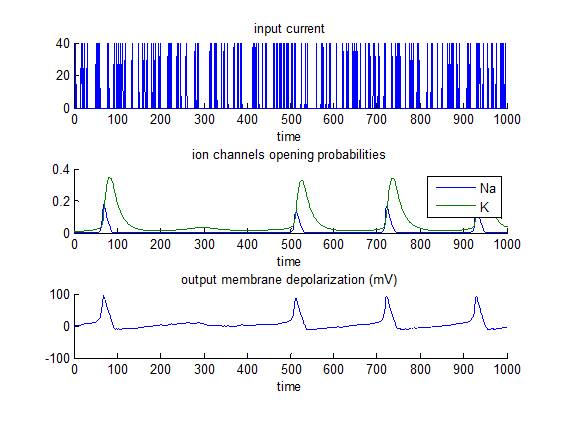
This is the most established model of spiking neurons, which was developed from Hodgkin and Huxley’s 1952 work based on data from the squid giant axon. In brief, short bursts of depolarizing input current are sent to a neuron that has a all-or-none response if the membrane depolarization reaches a critical threshold (approx. 80mV). The script demo_HodgkinHuxley.m simulates the response of such a neuron, and then inverts the model. Emphasis is put on the identifiability of model parameters (e.g. K/Na conductances).
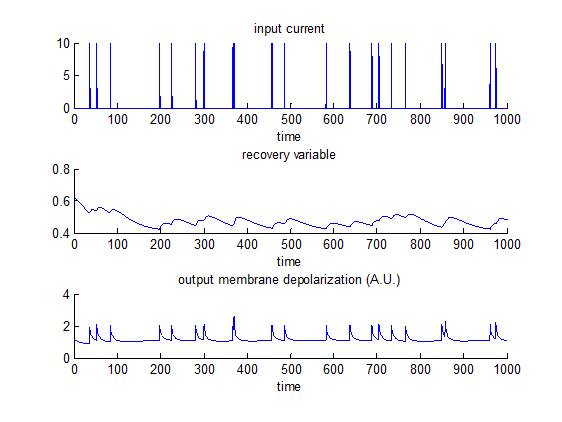
Fitzhugh-Nagumo model
This is essentially a reduction of the Hodgkin-Huxley model, which was introduced by FitzHugh and Nagumo in 1961 and 1962. In brief, the model captures the neuron’s “regenerative self-excitation” using a nonlinear positive-feedback membrane voltage, as well as its recovery dynamics using a linear negative-feedback gate voltage. Note that this does not generate ‘all-or-none’ spikes (as in the Hodgkin-Huxley model), but supra-threshold input create large deviations from equilibrium membrane depolarization. NB: an action potential approximately corresponds to a deviation of about 1 A.U. w.r.t. equilibrium. The script demo_FHN.m simulates the response of such a neuron, and then inverts the model. Emphasis is put on the identifiability of model parameters (e.g. recovery time constants). In contradistinction, the script demo_fitzhugh.m assesses whether one can use VBA’s stochastic inversion to identify the system’s input.