WIKI Dynamic Causal Modeling
- Crash-course on DCM
- Preparing a vanilla DCM analysis in VBA
- A few advanced tricks
- A few useful demonstration scripts
Crash-course on DCM
Decomposing the relation existing between cognitive functions and their neurobiological “signature” (the spatio-temporal properties of brain activity) requires an understanding of how information is transmitted through brain networks. The ambition here is to ask questions such as: “what is the nature of the information that region A passes on to region B”? This stems from the notion of functional integration, which views function as an emergent property of brain networks. Dynamic causal modelling or DCM was developed specifically to address this question.
What you cannot ignore
DCM embraces a graph-theoretic perspective on brain networks, whereby functionally segregated sources (i.e. brain regions or neuronal populations) correspond to “nodes” and conditional dependencies among the hidden states of each node are mediated by effective connectivity (directed “edges”). DCM generative models are causal in at least two senses:
- DCM describes how experimental manipulations influence the dynamics of hidden (neuronal) states of the system using ordinary differential equations. These evolution equations summarize the biophysical mechanisms underlying the temporal evolution of states, given a set of unknown evolution parameters that determine both the presence/absence of edges in the graph and how these influence the dynamics of the system’s states.
- DCM maps the system’s hidden states to experimental measures. This observation equation accounts for the main characteristics of the neuroimaging apparatus.
The inversion of such models given neuroimaging data can then be used to identify the structure of brain networks and their specific modulation by the experimental manipulation (i.e. induced plasticity). For example, showing that a given connection is modulated by the colour of some stimulus demonstrates that this connection conveys the colour information.
A unique equation for multiple effect types
As highligthed above, DCM relies on ordinary differential equations that specify how network nodes influence each other. For fMRI times series, the core DCM equation writes:
\[\frac{dx}{dt}=Ax + \sum_i u_i B^{(i)}x + Cu + \sum_j x_j D^{(j)}x\]where \(x\) is a vector of DCM hidden states that quantifies activity in each node of the relevant brain network and \(u\) are user-specified inputs that drive or modulate activity in network nodes. Matrices \(A\), \(B\), \(C\) and \(D\) correspond to connection strengths, input modulations of connections, input-state couplings and state modulations of connections, respectively. They are estimated by fitting the DCM model to fMRI time series (accounting for the fMRI temporal smearing induced by the neuro-vascular coupling).
You do not have to create an evolution function that implements DCM hidden states dynamics. This is because VBA already possesses a built-in function that does exactly this, namely:
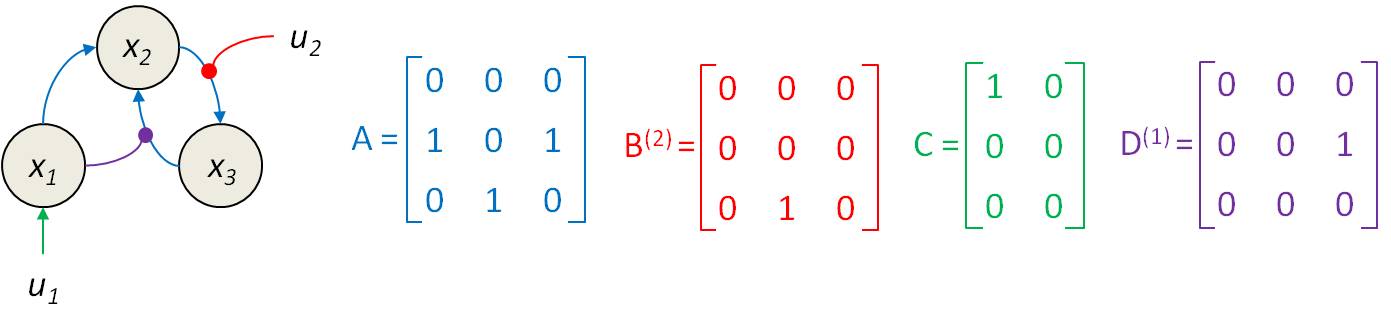
f_DCMwHRF.m. In addition, VBA also includes dedicated functions that were designed to facilitate the preparation of DCM analyses (see below). Nevertheless, DCM users have to specify which entries in \(A\), \(B\), \(C\) and \(D\) matrices are non-zero. We refer to this as setting the connectivity structure of the DCM model. The Figure above depicts the correspondance between the entries of DCM matrices and the underlying types of edges in a typical DCM network model. This example is detailed below. Note that DCM matrices are oriented such that directed edges go from columns to rows.
Preparing a vanilla DCM analysis in VBA
Recall that DCM has many variants, which may be specific to neuroimaging modalities (e.g., EEG/MEG, intracranial LFP, fMRI, etc…). Although almost all variants of DCM are directly available from the SPM academic freeware, only a few of them are already implemented in VBA. In particular, VBA includes DCM for fMRI time series. In what follows, we will briefly review how to prepare such vanilla DCM analysis.
Note: we refer the reader to the SPM documentation to help you design and preprocess a DCM-friendly experiment. See also Daunizeau et al; (2011), Optimizing experimental design for comparing models of brain function, PLoS Comp. Biol. 7(11): e1002280.
Extracting the fMRI timeseries
First, one needs to extract fMRI timeseries from relevant regions of interest or ROIs. This can be done easily in SPM:
- Locate the central voxel of each ROI, e.g., by selecting the peak of activation in the corresponding significant cluster.
- Click on SPM’s ‘eigenvariate’ button.
- Define the ROI geometry.
- Adjust for effects of interest, e.g., to correct for movement/physio artifacts.
- Save.
This procedure will provide a timeseries describing the ‘typical’ activity in the ROI. Repeat for each node.
For each subject, you will have to load all those timeseries and store them in the observation matrix y_fmri:
% load eigenvariates
data_ROI_1 = load('VOI_ROI1_1.mat') ;
data_ROI_2 = load('VOI_ROI2_1.mat') ;
data_ROI_3 = load('VOI_ROI3_1.mat') ;
% store in the observation matrix
y_fmri = [data_ROI_1.Y data_ROI_2.Y data_ROI_3.Y ]' ;
Specifying the inputs
The inputs to the DCM are in general identical to the (un-convolved) regressors used in SPM’s first level analysis. In VBA, one needs to store them in a matrix u that usually has the same number of columns as the data matrix (in case inputs are sampled at the fMRI rate) or more (if you define the inputs at the micro-time resolution).
Setting the connectivity
You now have to specify which entries of the DCM matrices are non-zero:
-
Static connectivity: The matrix \(A\) defines the network’s invariant connectivity (columns=source nodes, lines=target nodes). Its size is \(n \times n\), where \(n\) is the number of network nodes.
% node 1 projects on node 2 % node 2 projects on node 3 % node 3 projects on node 2 A = [0 0 0 ; 1 0 1 ; 0 1 0 ] ; -
Modulatory influences: The matrices \(B\) define potential psycho-physiological influences. In VBA, \(B\) is a cell-array (of size the number of inputs \(n_u\)), where each cell is a matrix of same size as \(A\) that specifies which network connection is modified by the corresponding input.
% the second input modulates the connection from node 2 to node 3 B{2} = [0 0 0 ; 0 0 0 ; 0 1 0 ] ; -
Direct inputs: The matrix \(C\) defines which input (columns) enters which node (lines). Its size is \(n \times n_u\), where \(n_u\) is the number of inputs:
% first input enters node 1 C = [1 0 ; 0 0 ; 0 0 ] ; -
Quadratic effects: The last set of matrices (namely: \(D\)) captures gating (interaction or quadratic) effects. In VBA, \(D\) is a cell-array (of size the number of nodes \(n\)), where each cell is a matrix of same size as \(A\) that specifies which network connection is modulated or gated by the corresponding node.
% node 1 modulates the feedback connection from node 3 to node 2 D{1} = [0 0 0 ; 0 0 1 ; 0 0 0 ] ;
Running the inversion
VBA contains evolution and observation functions for vanilla DCM analysis of fMRI time series. These require specific optional options.inF and options.inG structures, which can be directly derived from the above \(A\), \(B\), \(C\) and \(D\) matrices and a few other parameters. Simply call the prepare_fullDCM.m function:
%- prepare the DCM structure
TR = 2; % fMRI sampling resolution (in secs)
microDT = 1e-1; % micro_resolution = ODE solver time step (in secs)
homogeneous = 1; % enforces identical hemodynamic params across ROIs
options = prepare_fullDCM(A, B, C, D, TR, microDT, homogeneous);
This sets up VBA’s options structure, excluding DCM priors.
Default DCM priors can then be set automatically as follows:
nreg = 3; % number of network nodes
n_t = 720; % number of fMRI time samples
reduced_f = 1; % simplified HRF model
stochastic = 0; % for deterministic DCM
options.priors = getPriors(nreg,n_t,options,reduced_f,stochastic);
The main VBA inversion routine can now be called to run the DCM analysis:
f_fname = @f_DCMwHRF; % DCM evolution function
g_fname = @g_HRF3; % % DCM observation function
dim=options.dim;
[posterior,out] = VBA_NLStateSpaceModel(y,u,f_fname,g_fname,dim,options);
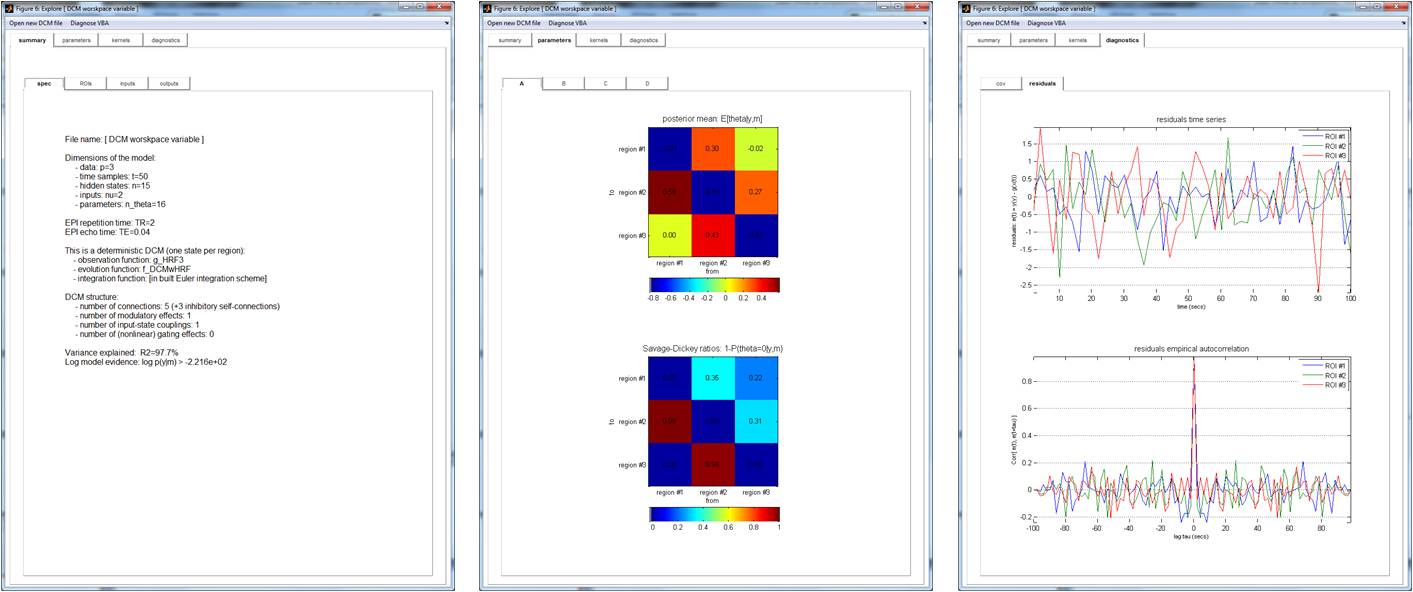
Inversion results can be eyeballed using standard VBA’s graphical output, or, alternatively, using DCM-specific tools (cf. function spm_dcm_explore.m described below).
Statistical inference on DCM parameters is strongly dependent upon one’s experimental design. In particular, it may be that some rest-connectivity parameters (i.e. elements of the \(A\) matrix) and hemodynamic parameters may be partly non-identifiable. We advise users to check potential non-identifiability issues using VBA diagnostic tools.
A few advanced tricks
Using SPM-specified structures in VBA (and back)
If you already performed a DCM analysis in SPM, you may have recognized that \(A\), \(B\), \(C\) and \(D\) matrices correspond to DCM.a, DCM.b, DCM.c, and DCM.d of the SPM-specified DCM structure, respectively. In fact, one can use the graphical user interface of SPM to specify a DCM, and then format the SPM structure for a VBA analysis. The following script allows one to invert an SPM-specified DCM model using VBA, and then eyeball inversion results and diagnostics:
[y, u, f_fname, g_fname, dim, options] = dcm2vba(DCM); % SPM-compatible format to VBA-compatible format
[posterior, out] = VBA_NLStateSpaceModel(y, u, f_fname, g_fname, dim, options); % VBA inversion
DCM = vba2dcm(posterior, out, [], TR); % VBA-compatible format to SPM-compatible format
spm_dcm_explore(DCM) % eyeball inversion results
where DCM is the variable saved in the SPM DCM-file and TR is the fMRI repetition time.
The graphical output of spm_dcm_explore.m is appended below:
Including confounds in DCM analyses
Some experimental designs may be associated with a few anticipated confounding factors. These typically take the form of mixtures of regressors that may induce sample-to-sample variations in the fMRI time series, above and beyond those that are modelled using DCM. VBA enables one to include these in the analysis as long as the corresponding “null design” matrix is known. For example, one may want to consider (non specific) slow trends, which may act as confounding factors. The following script exemplifies how to account for such confounds:
nconfounds = 16; % number of basis functions
btype = 'Fourier'; % basis function type
[X0] = get_U_basis(n_t*TR,TR,nconfounds,btype)'; % creates basis function set on temporal grid
[u,options,dim] = addConfounds2dcm(X0,u,options,dim); % modifies the i/o of DCM inversion
The options structure now contains the set of confounds (encoded in the “null design” matrix X0), whose impact on fMRI times series will be estimated along with other DCM parameters…
Of course, any kind of “null design” matrix can be included as confounds in DCM. Note that including these confounds in the generative model is not equivalent to removing them prior to performing the DCM analysis!
Stochastic DCM
By default, vanilla DCM analyses relY upon a deterministic model of neural dynamics (cf. ordinary differential equation above). However, VBA can be used to invert stochastic DCMs (Daunizeau et al., 2012), whereby unpredictable neural perturbations are allowed to interact with responses evoked by the experimental manipulation. In formal terms, the equation above is augmented with stochastic state noise, which has to be estimated, along with other DCM parameters, given fMRI time series. It turns out that the inversion of stochastic and deterministic systems are qualitatively different from each other. Nevertheless, switching to stochastic DCM
can be done simply by changing VBA’s priors on state noise precision, or, alternatively, by setting stochastic = 1 prior to calling getPriors.
Note: stochastic DCM are notoriously difficult to invert. We refer the interested reader to the following two relevant works:
A few useful demonstration scripts
A number of VBA demonstration scripts have been written for DCM:
demo_dcm_1region.m: this script simulates and inverts a 1-node network model. We advise readers to have a look at this demo in the aim of getting more insight on the statistical identifiability of connectivity parameters (including, e.g., local self-inhibitory connections) and neuro-vascular coupling parameters.demo_dcm4fmri.m: this script simulates and inverts a 3-nodes network model, with induced network plasticity. Emphasis is put on the influence of neural noise on the system’s dynamics.demo_dcm4fmri_distributed.m: this script simulates and inverts a 3-nodes network model (same as above). Here, the observation function has been augmented with unknown spatial profile of activation, which can be useful to capture non-trivial spatial encoding of experimentally controlled stimuli or observed behaviour.